- خانه
- درس امنیت شبکه
- برنامه نویسی موبایل
- برنامه نویسی موبایل2
- آموزش برنامه نویسی با فلاتر
- نرم افزارهای توسعه موبایل
- درس برنامه سازی پیشرفته
- تجزیه و تحلیل سیستم ها
- شبیه سازی کامپیوتری
- کار راه شغلی
- بانک های اطلاعاتی
- آزمایشگاه سیستم عامل
- مباحث ویژه
- ریاضیات مهندسی
- ساختمان داده
- گرافیک کامپیوتری 1
- زبان ماشین و اسمبلی
- سیستم عامل شبکه
- شبکه های کامپیوتری
- شبکه و برررسی ابزار های کالی
- شیوه ارائه مطالب
- درس پروژه / کارآموزی
- مهندسی نرم افزار
- هوش مصنوعی
- معماری کامپیوتر
- سیستم عامل
- برنامهنويسي سختافزار
- زبان تخصصی کامپیوتر
- محیط های چند رسانه ای
- دانلود جزوات و منابع
- پژوهش
- کارگاه های آموزشی آنلاین
- آموزش وردپرس
- پروژه ها
- لهجه قاینی
- کتابخانه میقات
- کنفرانس ها و فعالیت ها
- تصاویر طبیعی
- معرفی کتاب
- پادکست
- تماس با ما
پروژه ها
-
یکی از مباحث مهم در جامعه امروزی که دغدغه بسیاری از کارشناسان و همچنین کاربران می باشد بحث امنیت و تشخیص و تایید هویت است
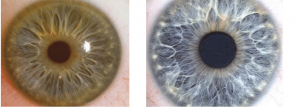
امروزه در امور مربوط به امنیت اماکنی مانند دانشگاه ها ، فرودگاه ها، وزارتخانه ها و حتی شبکه های کامپیوتری استفاده از روش های بیومتریک در تشخیص هویت یا تایید هویت افراد بسیار متداول شده است . سیستم های پیشرفته حضور و غیاب ادارات، سیستم های محافظتی ورود خروج اماکن خاص، نوت بوک های مجهز به Finger Print و … از روش های مختلف تشخیص هویت بیومتریک استفاده می کنند
-
چکیده: اجازه دهید هر مکان از لتیس مربعی 𝕫2 را به طور مستقل با احتمال p بسته و در غیر این صورت باز اعلام کرد. بازی زیر را در نظر بگیرید: یک علامت در مبدا شروع میشود، و دو بازیکن به نوبت از مکان فعلی خود، x، به یک مکان باز در {x+0,1, x+(0,1)} حرکت میکنند؛ اگر هر دو این مکان ها بسته باشد، در این صورت بازیکنی که باید حرکت کند بازی را میبازد. آیا احتمال اینکه این بازی به سمت بهترین بازی ممکن پیش برود مثبت است – یعنی هیچ یک از این دو بازیکن مجبور به پیروز شدن نباشند؟ این مساله با سوالی در رابطه با ارگادیک بودن (ارگادیک بودن) یک دستگاه سلولی احتمالاتی(PCA) معین ابتدایی و یک بعدی معادل است، که در زمینه شمارش حیوانات، زیر تغییر میانگین-طلایی (golden-mean subshift)، و مدل هسته سخت میباشد. ارگادیک بودن در PCA به عنوان یک مساله باز توسط نویسندگان مختلف مورد اشاره قرار گرفته است. ما ثابت میکنیم که PCA برای تمام مقادیر 0<p<1 ارگادیک است، و با همین نسبت بازی در 𝕫2 دارای هیچ تساوی نخواهد بود. ما نتایج مشابهی برای یک نوع تغییرات اشتباه خاص در بازی و PCA مربوط به آن ارایه میدهیم.
-
کلاسهبندی به روشی اطلاق میشود که به درستی کلاس هدف را برای یک نمونه بدون برچسب با استفاده از آموزش موارد شرح داده شده توسط مجموعهای از ویژگیها و یک برچسب پیش بینی مینماید. کلاسهبندی بر اساس عنوان به دلیل سادگی و عملکرد بسیار جذاب است. با این حال، بسیاری از این موارد نسبت به نویز حساسند و برای مسایل دنیای واقعی نامناسب میباشند. این مقاله یک نمونه جدید بر اساس الگوریتم کلاسهبندی را معرفی میکند که با عنوان کلاسهبندی بر اساس تطبیق الگو (PMC) شناخته میشود. اصل مهم در PMC کلاسهبندی نمونههای بدون برچسب، مطابق با الگوهای موجود در مجموعه دادههای آموزشی میباشد. مزیت استفاده از PMC نسبت به سایر روشهای مبتنی بر نمونه، روش کلاسهبندی ساده همراه با عملکرد بالا است. به منظور بهبود دقت کلاسهبندی PMC، بهینه سازی کلونی مورچه مبتنی بر الگوریتم انتخاب ویژگیهای بر اساس ایده PMC مطرح شده است. کلاسهبندی برروی 35 مجموعه داده ارزیابی شده است. نتایج تجربی نشان میدهد که PMC مشابه با بسیاری از روشهای کلاسهبندی بر اساس مثال، عملکرد مناسبی دارد. نتایج با استفاده از آزمونهای آماری ناپارامتری نیز مورد بررسی قرار گرفت. همچنین، زمان ارزیابی PMC در مقایسه با زمان روشهای مبتنی بر گرانش مورد استفاده برای کلاسه بندی کمتر میباشد.
-
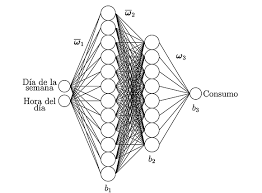
در این مطالعه، نوعی پرسپترون انشار بازگشتی آموزشی چندلایه مبتنی بر PSO به منظور طبقهبندی دادهها ارائه شده است. روش ارائه شده با مجموعه دادههای مختلف از منبع یادگیری ماشین UCI تست شده است. ادامه این مقاله به صورت زیر سازمان یافته است. بخش 2 برخی از مفاهیم اساسی مانند PSO و MLP را معرفی میکند. بخش 3 به ارایه روش کار پیشنهادی میپردازد. بخش 4 دربردارنده تنظیمات تجربی و نتایج ارائه شده، است. بخش 5 مشتمل بر نتیجهگیری و کارهای قابل انجام آینده است.
-
برای انجام این کار از روشهای under sampling کلاس اکثریت و یا over sampling کلاس اقلیت استفاده میشود. سپس دادهای متوازن شده را برای آموزش طبقه بند مورداستفاده قرارمی دهند. این عمل منجر به ایجاد الگوهای موردعلاقه برای انجام عمل طبقهبندی میشود. از طرفی با انجام متوازن کردن کلاسها، میتوان مقدار پارامتر AUC را افزایش داد. AUC یک کمیت اندازهگیری خوب برای بیان میزان کارایی طبقهبندی است. در این مقاله، ما با استفاده از روشهای جداسازی الگوهای مرزی و غیر مرزی، کلاس اکثریت و اقلیت را به این دو مجموعه تبدیل میکنیم. تحت عمل under sampling الگوهای مرزی کلاس اکثریت را حذف میکنیم. این بهنوعی باعث متوازن شدن دیتاست نامتوازن میشود. نتیجه اینکه کمیت AUC بهبود داده میشود. آزمایشهای انجامشده بهبود AUC را نسبت به سایر الگوریتمها نشان میدهد.